PENERAPAN TURUNAN: KEMONOTONAN, INTERVAL FUNGSI NAIK/TURUN, KECEKUNGAN DAN UJI TURUNAN KEDUA

 Kemonotonan fungsi adalah salah satu materi yang termasuk kedalam penggunaan turunan (pada buku kalkulus edisi 5 jilid 1). Materi ini digunakan untuk melihat naik turunya suatu grafik fungsi.

Kemonotonan grafik fungsi akan mudah dipahami jika kamu sudah mengenal materi selang/interval. Soal kemonotonan fungsi biasanya menanyakan pada interval berapa fungsi tersebut naik dan pada interval berapa fungsi tersebut turun.

Kemonotonan fungsi sederhananya seperti ini, suatu fungsi dikatakan monoton jika fungsi tersebut naik terus ataupun turun terus pada suatu selang/interval.

Teorema berikutnya menunjukkan bagaimana penggunaan turunan kedua suatu fungsi untuk menentukan selang di mana grafik f tersebut cekung ke atas atau cekung ke bawah. Bukti teorema ini merupakan akibat langsung dari Teorema Uji Fungsi Naik dan Turun, dan definisi kecekungan.

Adapun kurva fungsi naik dan fungsi turun dapat kita amati pada gambar di bawah ini.

Fungsi f selalu naik pada interval I, jika memiliki sifat: f'(x)>0 

Fungsi f selalu turun pada interval I, jika memiliki sifat: f'(x)<0 

Fungsi f tidak pernah turun pada interval I, jika memiliki sifat: f'(x)≥0 

Fungsi f tidak pernah naik pada interval I, jika memiliki sifat: f'(x)≤0

Kecekungan

Karakteristik suatu fungsi yang naik atau turun dapat kita gunakan untuk mendeskripsikan grafik fungsi tersebut. Selain itu, apabila kita tahu dimana letak selang yang membuat f ’ naik atau turun maka kita dapat menentukan di mana grafik fungsi f akan cekung ke atas atau cekung ke bawah.

Definisi Kecekungan

Misalkan f terdiferensialkan pada selang buka I. Grafik f akan cekung ke atas pada I jika f ’ naik pada selang tersebut dan akan cekung ke bawah pada I jika f ’ turun pada selang tersebut.

Interpretasi grafis kecekungan dari suatu fungsi berikut akan sangat berguna.

1. Misalkan f terdiferensialkan pada selang buka I. Jika grafik f cekung ke atas pada I, maka grafik f berada di atas semua garis singgungnya pada selang tersebut. (Lihat gambar (a) di bawah).
2. Misalkan f terdiferensialkan pada selang buka I. Jika grafik f cekung ke bawah pada I, maka grafik f berada di bawah semua garis singgungnya pada selang tersebut. (Lihat gambar (b) di bawah).

Untuk menemukan selang buka di mana suatu grafik fungsi f cekung ke atas atau cekung ke bawah, kita harus menemukan selang di mana f ’ naik atau turun. Sebagai contoh, grafik

akan terbuka ke bawah pada selang buka (–∞, 0) karena

turun pada selang tersebut. Demikian pula, grafik f akan cekung ke atas pada selang (0, ∞) karena f ’ naik pada selang tersebut. Perhatikan gambar di bawah.

Turunan Kedua
Turunan kedua dapat digunakan untuk menentukan jenis-jenis nilai stasionernya. Sebenarnya dari turunan pertama kita telah dapat mengetahuinya dengan menguji tanda-tandanya. Hal ini kadang terasa aga merepotkan, dengan menggunakan turunan kedua menentukan jenis-jenis nilai stasioner suatu fungsi akan lebih mudah. Dalam menentukan jenis nilai stasioner dengan menggunakan tes turunan kedua berlaku

Misalkan f$f$(x)$(x)$ kontinu pada interval b<x<c$b<x<c$ yang memuat x=a$x=a$. 

Turunan pertama 

f′(x)$f^{\prime }(x)$ dan turunan kedua f′′(x)$f^{″}(x)$ terdefinisi dalam interval tersebut dan f′(a)=0$f^{\prime }(a)=0$, 

maka Jika 

f′′(x)<0$f^{″}(x)<0$, maka f(a)$f(a)$ adalah nilai balik naksimum
Jika f′′(x)>0$f^{″}(x)>0$, maka f(a)$f(a)$ adalah nilai balik minimum

Namun, ada hal yang perlu diperhatikan dalam menggunakan uji turunan kedua, jika f′′x=0$f^{″}x=0$ atau tak terhingga, maka jenis-jenis nilai stasionernya tidak dapat ditentukan. Apabila demikian, jenis-jenis nilai stasionernya hanya dapat digunakan dengan menggunakan uji turunan pertama saja.

soal pilihan ganda dan pembahasannya yang berkaitan dengan penerapan Turunan

1. Tentukan persamaan garis singgung kurva y = f (x) =  5x² – 3x  di titik (2, 14) adalah. . . 

Jawaban :

2. Tentukan koordinat titik singgung dari garis singgung kurva y = f ( x ) = 3x² – 3x + 1 yang bergradien 15 adalah . . .

Jawaban :

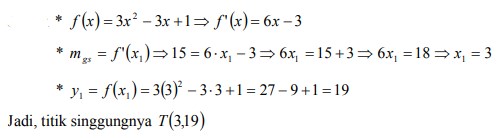
3. Tentukan persamaan garis singgung kurva f(x) = x² + 2x – 3 yang sejajar garis y = -2x + 5 adalah. . .

Jawaban : 

4. Tentukan persamaan garis singgung kurva f ( x ) = x² + 4x + 2 yang tegak lurus garis x – 2y + 6 = 0 adalah . . .

Jawaban : 

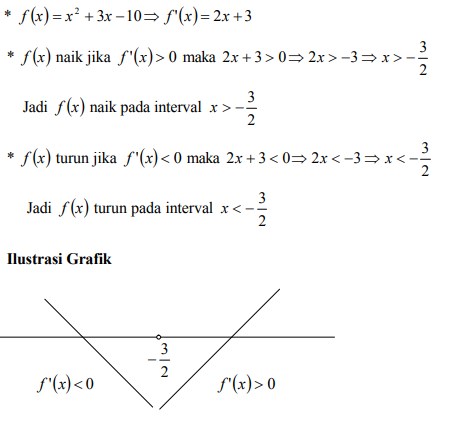
5. Tentukan interval dimana f (x) naik dan f (x) turun dari fungsi f ( x ) = x²  + 3x – 10

Jawaban : 

6. Tentukan interval fungsi naik dan fungsi turun dari 

Jawaban : 

7. Tentukan titik stasioner dan jenisnya dari fungsi f (x) = 2x³ – 9x² + 12x adalah . . .

Jawaban : 

8. Fungsi f (x) = ax³ + bx² memiliki titik stasioner (1, -1) tentukan nilai a dan b adalah . . .

Jawaban : 

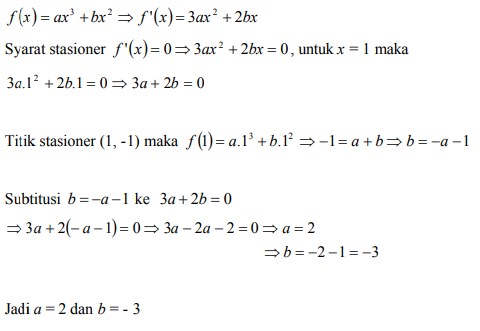
9. Tentukan nilai maksimum dan minimum dari fungsi f (x) = 2x³ + 15x² + 36x dalam interval 1 ≤ x ≤ 5

Jawaban : 

Dari nilai-nilai tersebut dapat kita lihat bahwa nilai maksimumnya adalah 55 dan nilai minimumnya adalah 23.

Penerapan Nilai Maksimum dan Minimum dalam Kehidupan Sehari-hari

10. Kebun Pak Subur berbentuk persegi panjang dengan kelilingnya 60 meter. Jika panjangnya x meter dan lebarnya y meter, tentukan:

a. Persamaan yang menyatakan hubungan antara x dan y

b. Ukuran kebun Pak Subur agar luasnya maksimum.

Jawaban : 

Dengan menguji nilai L'(x) menggunakan garis bilangan, diperoleh