Skip to main content

INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

 

INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA 


Pengertian Integral

\int kx^n \, dx = \frac{k}{n+1} x^{n+1 }+ C

Keterangan

k : koefisien
x : variabel
n : pangkat/derajat dari variabel
C : konstanta

Pengertian Integral secara sederhana yaitu invers (kebalikan) dari suatu turunan. Penjebaran lebih luasnya adalah sebuah konsep bentuk penjumlahan berkesinambungan dan bersama dengan inversnya.

Ide integral sendiri muncul ketika matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi.

Sifat Integral

Berikut ini beberapa sifat integral.

\int_a^a f(x) \, dx = 0

\int_a^b f(x) \, dx = - \int_b^a f(x) \, dx

\int_a^b k f(x) \, dx = k \int_a^b f(x) dx

\int_a^b (f(x) + g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx

\int_a^b (f(x) - g(x)) \, dx = \int_a^b f(x) \, dx - \int_a^b g(x) \, dx

Jika a<b<c, maka

\int_a^c f(x) \, dx = \int_a^b f(x) + \int_b^c f(x)

 

Jenis Integral

Seperti yang sudah dijelaskan sebelumnya, terdapat 2 Jenis Integral, yaitu: Integral Tak Tentu dan Integral Tentu

Integral Tak Tentu

Integral Tak Tentu adalah pengintegralan fungsi f(x) apabila turunannya telah diketahui.

  • Cara Membaca Integral Tak Tentu

Setelah membaca uraian di atas, taukah kalian cara membaca kalimat integral? Integral di baca seperti ini:

baca yang di baca Integral Tak Tentu Dari Fungsi f(x) Terhadap Variabel X.

Rumus Umum Integral

Berikut ini adalah rumus umum yang ada pada integral:

Rumus Umum Integral

  • Pengembangan Rumus Integral

Pengembangan Rumus Integral

 

Integral Tak Tentu Fungsi Aljabar

Mari perthatikan baik-baik contoh dari beberapa turunan dalam fungsi aljabar di bawah ini:

  • Turunan dari fungsi aljabar y = x3 adalah yI = 3x2
  • Turunan dari fungsi aljabar y = x3 + 8 adalah yI = 3x2
  • Turunan dari fungsi aljabar y = x3 + 17 adalah yI = 3x2
  • Turunan dari fungsi aljabar y = x3 – 6 adalah yI = 3x2

 

Rumus

Berikut ini Rumus dari Integral Tak Tentu

\int f(x) \, dx = F(x) + C

Keterangan

f(x) = persamaan kurva
F(x) = luasan di bawah kurva f`(x)
C = konstanta

Sifat

Pada integral tak tentu berlaku sifat berikut

\int ax^n \, dx = \frac{a}{n+1}x^(n+1)+C

\int k f(x) \, dx = k \int f(x) dx

\int (f(x) + g(x)) \, dx = \int f(x) \, dx + \int_a^b g(x) \, dx

\int (f(x) - g(x)) \, dx = \int f(x) \, dx - \int_a^b g(x) \, dx

Contoh

Berikut ini contoh dari Integral Tak Tentu

\int (2x+5)dx = 2x^2+5x+c

\int (3x-3)dx = x^3-5x+c

 

Integral Tak Tentu Fungsi Trigonometri

Pada fungsi trigonometri berlaku integral tak tentu sebagai berikut

\int cos x \, dx = sin x + C

\int sin x \, dx = - cos x + C

\int cos(ax+b)dx = \frac{1}{a}sin(ax+b)+C

\int sin(ax+b)dx = - \frac{1}{a}cos(ax+b)+C

 

Contoh Soal Integral

Soal 1

Pembahasan

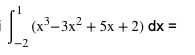
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi  3x2 + 5x + 2 menjadi seperti di bawah ini.

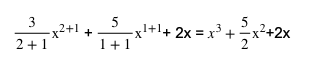
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.

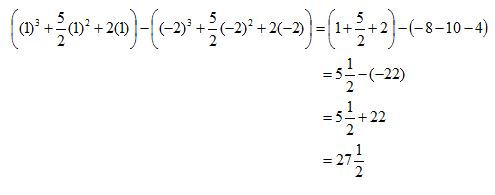
Contoh Soal Integral no 1

Hasil dari integral tersebut adalah 27,5.

Soal 2.

Diketahui turunan y = f(x) adalah = f ‘(x) = 2x + 3

Jika kurva y = f(x) lewat titik (1, 6), maka tentukan persamaan kurva tersebut.

Jawab:

f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.

Kurva melalui titik (1, 6), berarti f(1) = 6 hingga dapat di tentukan nilai c, yakni 1 + 3 + c = 6 ↔ c = 2.

Maka, persamaan kurva yang dimaksud yaitu:

y = f(x) = x2 + 3x + 2.

Soal 3.

Carilah hasil dari ʃ21 6x2 dx !

Pembahasan
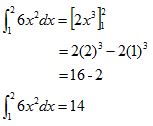
Contoh Soal Integral Tentu no 1

Jadi, hasil dari ʃ21 6x2 dx adalah 14.

Soal 4

Gradien garis singgung kurva pada titik (x, y) ialah 2x – 7. Apabila kurva itu melewati titik (4, –2), maka tentukanlah persamaan kurvanya.

Jawab:

f ‘(x) = = 2x – 7
y = f(x) = ʃ (2x – 7) dx = x2 – 7x + c.

Sebab kurva melewati titik (4, –2)
maka:

f(4) = –2 ↔ 42 – 7(4) + c = –2
–12 + c = –2
c = 10

Maka, persamaan kurva tersebut yakni:

y = x2 – 7x + 10.

Berapakah nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx ?


Pembahasan
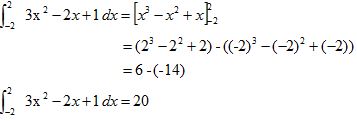
Contoh Soal Integral Tentu no 3

Jadi, nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx adalah 20.

Soal 5.

Hitunglah nilai integral tentu dari ʃ94 1/√x dx !

Pembahasan
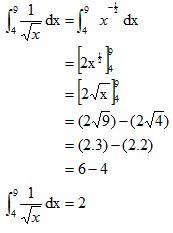
Contoh Soal Integral Tentu no 4

Jadi, nilai integral tentu dari ʃ94 1/√x dx adalah 2.

Comments

Post a Comment

Popular posts from this blog

SOAL TRANSFORMASI DAN PENYELESAIANNYA

1. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . . Jawaban : C Pembahasan :  Jawabannya adalah C 2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….  A. y = x² – 2x – 3  B. y = x² – 2x + 3 C. y = x² + 2x + 3 D. x = y² – 2y – 3 E. x = y² + 2y + 3 Jawaban : D Pembahasan :  Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri. pencerminan terhadap garis y = -x Jawabannya adalah D 3. Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks   adalah….  A. x² + y² – 6x – 4y- 3 = 0 B. X² + y² – 6x + 4y- 3 = 0 C. x² + y² + 6x – 4y- 3 = 0 D. x² + y² – 4x + 6y- 3 = 0 E. x² + y² + 4x – 6y+ 3 = 0 Jawaban : A Pembahasan :  Jawabannya adalah A 4. T 1  dan T 2  adalah transformasi yang masing-masing bersesuaian dengan  Ditentukan T = T 1  o T 2  , m...
Post a Comment
Read more

Jawaban soal limit turunan dan integral no 11

Post a Comment
Read more

PENERAPAN TURUNAN: KEMONOTONAN, INTERVAL FUNGSI NAIK/TURUN, KECEKUNGAN DAN UJI TURUNAN KEDUA

  Kemonotonan fungsi adalah salah satu materi yang termasuk kedalam penggunaan turunan (pada buku kalkulus edisi 5 jilid 1). Materi ini digunakan untuk melihat naik turunya suatu grafik fungsi. Kemonotonan grafik fungsi akan mudah dipahami jika kamu sudah mengenal materi selang/interval. Soal kemonotonan fungsi biasanya menanyakan pada interval berapa fungsi tersebut naik dan pada interval berapa fungsi tersebut turun. Kemonotonan fungsi sederhananya seperti ini, suatu fungsi dikatakan monoton jika fungsi tersebut naik terus ataupun turun terus pada suatu selang/interval. Teorema berikutnya menunjukkan bagaimana penggunaan turunan kedua suatu fungsi untuk menentukan selang di mana grafik  f  tersebut cekung ke atas atau cekung ke bawah. Bukti teorema ini merupakan akibat langsung dari Teorema Uji Fungsi Naik dan Turun, dan definisi kecekungan. Adapun kurva fungsi naik dan fungsi turun dapat kita amati pada gambar di bawah ini. Fungsi f selalu naik pada interval I, jika m...
Post a Comment
Read more