PENGERTIAN LIMIT
Pada dasarnya limit digunakan untuk menyatakan sesuatu yang yang nilainya mendekati nilai tertentu, seperti tak hingga yang pada dasarnya adalah angka yang sangat besar yang nilainya tidak dapat dipastikan. Limit menjelaskan suatu fungsi jika batas tertentu didekati. Jika suatu fungsi tidak terdefinisi untuk titik tertentu, tetapi kita masih bisa mencari nilai yang didekati oleh fungsi tersebut apabila titik tertentu makin didekati yaitu dengan limit.
Keterangan :
- Apabila x mendekati a tetapi x tidak sama dengan a maka f(x) mendekati L
- Pendekatan x ke a bisa dilihat dari dua sisi yaitu pada sisi kiri dan sisi kanan ataupun dengan kata lain x bisa mendekati dari arah kiri dan arah kanan hingga menghasilkan limit kiri serta limit kanan
Toerema / Pernyataan:

- Fungsi dikatakan mempunyai limit apabila antara limit kiri dan limit kananya mempunyai besar nilai yang sama
- Apabila limit kiri dan limit kanan tidak sama maka nilai limitnya tidak ada.

Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu:
Bentuk pertama
Bentuk kedua
Dalam hubungannya dengan bentuk limit yang pertama ada beberapa metode dalam menentukan nilai limit fungsi aljabar yaitu dengan cara substitusi dan cara pemfaktoran.
1. Cara Substitusi
Cara substitusi ini langkahnya dengan mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya. Berikut adalah beberapa contoh yang dapat dipahami.
Contoh 1:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh 2:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh soal 3:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh soal 4:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh soal 5:
Tentukan nilai limit fungsi aljabar dari,
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh 6:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh 7:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
2. Cara Pemfaktoran
Cara pemfaktoran digunakan apabila cara substitusi menghasilkan nilai limit yang tidak terdefinisikan seperti pada contoh berikut:
Cara pemfaktoran dilakukan dengan langkah menentukan faktor persekutuan antara pembilang dan penyebuntya. Berikut beberapa contoh untuk dipahami.
Contoh 1:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh 2:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh 3:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh soal 4:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh soal 5:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Dalam hubungannya dengan bentuk limit yang kedua ada beberapa cara dalam menentukan nilai limit fungsi aljabar yaitu metode membagi dengan pangkat tertinggi penyebut dan metode mengalikan dengan faktor sekawan.
1. Metode membagi dengan pangkat tertinggi penyebut
contoh 1:
Tentukan nilai limit fungsi aljabar dari
Besar pangkat pembilang dan penyebut dalam soal ini adalah 2, maka
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh 2:
Tentukan nilai limit fungsi aljabar dari
Besar pangkat pembilang dan penyebut dalam soal ini adalah 3, maka
Jadi, nilai dari limit fungsi aljabar tersebut,
Contoh soal 3:
Tentukan nilai limit fungsi aljabar dari
Besar pangkat pembilang dan penyebut dalam soal ini adalah 3, maka
Jadi, nilai dari limit fungsi aljabar tersebut,
2. Metode mengalikan dengan faktor sekawan
Contoh soal:
Tentukan nilai limit dari![]()
Langkah awal yang perlu dilakukan untuk menentukan nilai suatu limit yaitu dengan mensubtitusikan x=c ke f(x), sehingga dalam kasus ini substitusikan
x=4 ke ![]()
Setelah disubstitusikan ternyata nilai limit tersebut tidak terdefinisi atau merupakan bentuk tak tentu![]() . Maka dari itu untuk menentukan nilai suatu limit harus menggunakan metode lain. Apabila diperhatikan, pada f(x) terdapat bentuk akar yaitu
. Maka dari itu untuk menentukan nilai suatu limit harus menggunakan metode lain. Apabila diperhatikan, pada f(x) terdapat bentuk akar yaitu![]() sehingga metode perkalian dengan akar sekawaran dapat dilakukan pada kasus seperti ini.
sehingga metode perkalian dengan akar sekawaran dapat dilakukan pada kasus seperti ini.
Bentuk ![]() dapat difaktorkan menjadi
dapat difaktorkan menjadi ![]()
Jadi, nilai limit fungsi aljabar tersebut adalah -4
Sumber :
http://bunyan.co.id/materi-limit-fungsi-aljabar/



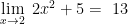














Comments
Post a Comment