BARISAN ARITMATIKA
Barisan Aritmatika (Un) adalah barisan bilangan yang memiliki pola yang tetap. Nah, polanya itu bisa berdasarkan operasi penjumlahan atau pengurangan. Jadi, setiap urutan suku memiliki selisih atau beda yang sama. Selisih inilah yang dinamakan beda. Biasa disimbolkan dengan b.
Misalnya, di suatu barisan memiliki suku pertama, yaitu 2. Suku pertama disimbolkan dengan U1 atau a. Lalu, di suku kedua (U2), yaitu 5. Suku ketiga (U3), yaitu 8, dan seterusnya. Berarti, barisan ini memiliki beda 3 pada setiap sukunya.
2, 5, 8, ...
(setiap suku memiliki selisih atau beda, yaitu 3)
Untuk mengetahui nilai suku ke-n dari suatu barisan arimatika dapat dihitung dengan rumus berikut.
Contoh Soal Barisan Aritmatika
1. Nilai 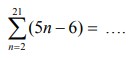
A. 882
B. 1030
C. 1040
D. 1957
E. 2060
Jawaban : B
Pembahasan :
2. Suku keempat dan suku ketujuh barisan aritmetika berturut-turut adalah 17 dan 29. Suku ke 25 barisan tersebut adalah….
A. 97
B. 101
C. 105
D.109
E. 113
Jawaban : B
Pembahasan :
3. Suatu deret aritmetika, diketahui jumlah 5 suku yang pertama = 35 dan jumlah 4 suku yang pertama = 24, suku yang ke 15 = ….
A. 11
B. 25
C. 31
D. 33
E. 59
Jawaban : C
Pembahasan :
4. Dari suatu barisan aritmetika, suku ketiga adalah 36, jumlah suku kelima dan ketujuh adalah 144. Jumlah 10 suku pertama deret tersebut adalah…
A. 840
B. 660
C. 640
D. 630
E. 315
Jawaban : B
Pembahasan :
5. Jumlah n suku pertama dari sebuah deret aritmetika adalah 1 n (3n – 1). Beda dari barisan aritmetika itu 2 adalah….
A. -3
B. -2
C. 3
D. 2
E. 4
Jawaban : C
Pembahasan :
Jumlah n suku pertama :

DERET ARITMATIKA
Deret aritmatika (Sn) adalah jumlah suku ke-n pada barisan aritmatika. atau bisa juga diartikan sebagai pola bilangan berderet di dalam matematika, yang mempunyai manfaat sangat penting dalam berbagai hal.
Secara konsep sebenarnya untuk deret aritmatika ini sederhana karena kita hanya menjumlahkan Barisan aritmatika yang sudah kita bahas sebelumnya sampai suku ke-n tergantung apa yang diperintahkan.
Dengan,
a adalah suku pertama
b adalah beda
Sn adalah jumlah suku ke-n
Contoh Soal Deret Aritmatika
1. Tentukanlah nilai dari suku ke-35 dari barisan deret aritmatika seperti berikut ini : 2, 4 , 6, 8 , … ?
A. 54
B. 45
C. 70
D. 74
E. 75
Penyelesaiannya :
Diketahui : Deret aritmatika: 2, 4, 6, 8, …
Jawaban :
a = 2
b = 4-2 = 2
Un = a + (n-1) b
Un = 2 + (35-1) 2
Un = 2 + (34).2
Un = 2 + 68
Un = 70
Jadi nilai pada suku ke-35 (U35) ialah 70. (C)
2. Diketahui pada suatu deret aritmatika : 3, 6, 12, 27, …., hitunglah beda dan suku ke-8 dari contoh deret aritmatika tersebut..
A. Beda 3, U8 =24
B. Beda 3, U8 =31
C. Beda 2, U8 =45
D. Beda 4, U8 =22
E. Beda 4, U8 =32
Penyelesaiannya :
Diketahui : Deret aritmatikanya: 3, 6, 12, 27, …
Ditanya : b dan U8 ?
Jawaban :
b = 6 – 3 = 3
Un = a + (n-1) b
Un = 3 + (8-1) 3
Un = 3 + (7).3
Un = 3 + 21
Un = 24
Jadi nilai dari bedanya adalah 3 dan nilai untuk Suku ke-8 adalah 21 (A)
3. Misalkan diketahui nilai dari suku ke-16 pada suatu deret arimatika adalah 34 dengan beda nya adalah 3, maka hitnglah U1 nya?
A. 6
B. 7
C. 10
D. 4
E. 12
Penyelesaiannya :
Diketahui :
U16 = 34
b = 3
n = 16
Ditanya : Nilai U1 ?
Jawaban :
Un = a + (n-1) b
U16 = a + (16-1) 3
34 = a + (15).3
34 = a + 30
a = 34 – 30
a = 4
Jadi nilai dari U1 Pada soal tersebut adalah 4. (D)
4. HitungLah jumlah nilai dari suku ke-5 (S5) dari deret aritmatika berikut ini : 4, 8, 16, 24, ….?
A. 32
B. 60
C. 87
D. 98
E. 120
Penyelesaiannya :
Diketahui :
a = 4
b = 8 – 4 = 4
n = 5
Ditanya : Jumlah pada suku ke-5 (S5) ?
Jawaban :
Un = a + (n-1) b
Un = 4 + (5-1)4
Un = 4 + 16
Un = 20
Sn = 1/2 n ( a + Un )
S5 = 1/2 .5 (4 +20)
S5 = 5/2 (24)
S5 = 60
Jadi jumlah nilai pada suku ke-5 dari deret aritmatika tersebut adalah : 60. (B)
5. HitungLah jumlah nilai dari suku ke-8 (S8) dari deret aritmatika berikut ini : 5, 10, 15, 20, ….?
A. 32
B. 180
C. 187
D. 98
E. 20
Penyelesaiannya :
Diketahui :
a = 5
b = 10 – 5 = 5
n = 8
Ditanya : Jumlah pada suku ke-8 (S8) ?
Jawaban :
Un = a + (n-1) b
Un = 5 + (8-1)5
Un = 5 + 35
Un = 40
Sn = 1/2 n ( a + Un )
S8 = 1/2 .8 (5 +40)
S8 = 8/2 (45)
S8 = 180
Jadi jumlah nilai pada suku ke-8 dari deret aritmatika tersebut adalah : 180. (B)







Comments
Post a Comment